Proof Of Fractional Exponents

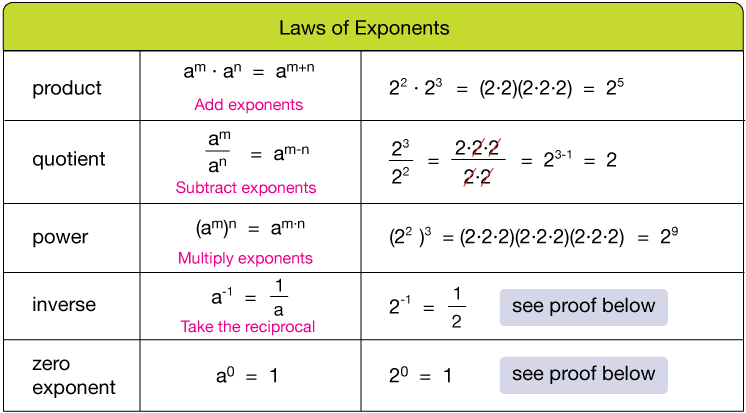
If x a x b x a b then x 05 x 05 x. But this property of exponents is the.

Simplifying Quotient Of Powers Rational Exponents Algebra Video Khan Academy

Examples in this section we will be restricted to integer exponents.

Proof of fractional exponents. There are two ways to simplify a fraction exponent such frac 2 3. Let x y be not negative a 1 and b odd. One part is 106 and another is 102.

A base number raised to some exponent or the value answer you get if you calculate a number raised to some exponent. But since 1 1 1 and 1 1 1 with 1 is not equal to 1 how can we say that x x 05 just because it follows an existing trend. The Formal Rules of Algebra Summary of the formal rules of algebra on the set of real numbers 1.

We will give the basic properties of exponents and illustrate some of the common mistakes students make in working with exponents. This algebra 2 video tutorial explains how to simplify fractional exponents including negative rational exponents and exponents in radicals with variables. Since one can integrate fractional exponents.

In this section we will start looking at exponents. Y b x y x b. Multiplying fractions with exponents with different bases and exponents.

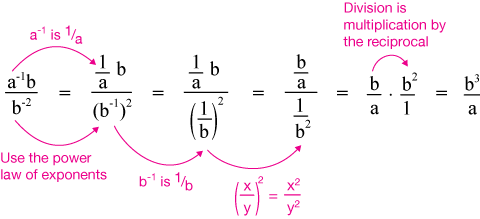
We also presume that the addition of exponents in products of powers of a radix applies to positive fraction exponents as well as integer exponents. For reference purposes this property is anm anm a n m a n m. The one we see here has a 1 in the numerator.

The online proofs Ive seen for fractional exponents goes as follows. To make a problem easier to solve you can break up the exponents by rewriting them. Now let x y be not negative and b d odd.

The exponent is the little elevated number. 16-week Lesson 15 8-week Lesson 11 Equations with Fractional Exponents 2 Steps for Solving Equations with Fractional Exponents. So it doesnt make sense to prove it that way.

A fractional exponent is an alternate notation for expressing powers and roots together. Now were going to think of slightly more complex fractional exponents. A power is the whole thing.

Convert from a fractional exponent to a radical 3. Now were going to see something different. Its easy to imagine how it works for non-fractional exponents.

What about functions with fractional exponents such as y x 23. The binomial theorem says nothing about fractional exponents. For example 8 is a power of 2 since 2 3 8.

In a fractional exponent think of the numerator as an exponent and the denominator as the root Another rule for fractional exponents. When we expand it we can see that. 01 is part of the proof of the negative exponent conjecture.

See the example below. Solve for the variable by using roots andor exponents principle of. Therefore x 05 x.

A nm b nm a b nm. The general form of a fractional exponent is x mn where x is the base and mn is the exponent. In this case 3 is the exponent and 2.

The binomial theorem for integer exponents can be generalized to fractional exponents. So he must be using a Taylor expansion but to find the Taylor expansion of tex 1 frac dx xfrac 1 2 tex one must know what the derivative of x½ is. Then This is seen to be consistent with the Power Rule for n 23.

In this case y may be expressed as an implicit function of x y 3 x 2. We will first rewrite the exponent as follows. You can either apply the numerator first or the denominator.

3 fractional derivatives are treated by riemann in the complex case by the cauchy integral formula which changes the order of the derivative into the order of an exponent under the integral sign. This is the same as x x. Since x a b b x a and by your proof for integer exponents x b a b x b a b x a we have x a b x b a.

Below is a specific example illustrating the formula for fraction exponents when the numerator is not one. Since logarithms are basically powers we can say that for example 1062106102. So lets see how to deal with a general rational exponent.

Rational exponents will be discussed in the next section. Dividing fractional exponents with same fractional exponent. Bm n b1 nm b m n b 1 n m In other words we can think of the exponent as a product of two numbers.

The axioms of equality a a Reflexive or Identity. Look at the figure given below to understand how fractional exponents are represented. Now let x y not negative a be arbitrary and b odd.

A b n c d m. The associated Maclaurin series give rise to some interesting identities including generating functions and other applications in calculus. Lets make a generalization of this example.

Then any product of powers of a radix z whose sum of exponents equals one must be derived from the sum of fractional exponents. Few examples of fractional exponents are 2 12 3 23 etc. So what I want to do is think about what 64 to the 23 power is.

Y x 1 b d e f. 43 3 12 2 237 025 05925. For example the following are equivalent.

Isolate the variable that has a fractional exponent 2. And here Im going to use a property of exponents that well study more later on.

What Do Fractional Exponents Mean By Brett Berry Math Hacks Medium

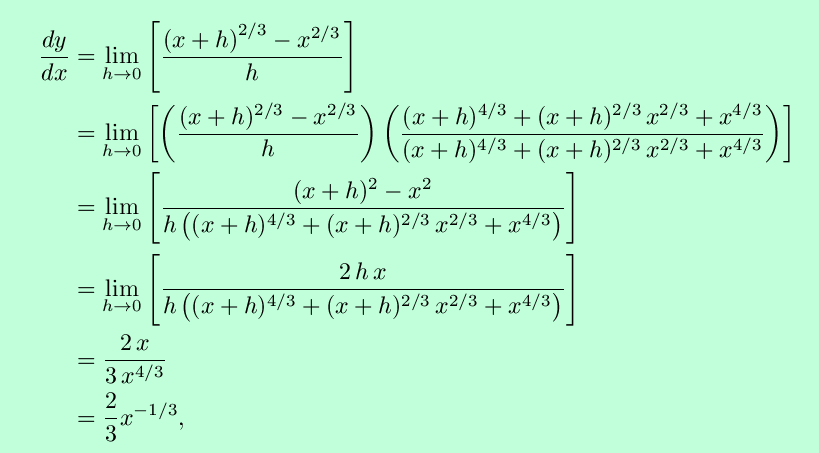
World Web Math Fractional Exponents

Fractional Exponents Rule Explained Youtube

What Are The Laws Of Rational Exponents Mathematics Stack Exchange

Power Rule For Differentiation Negative And Fractional Exponents Youtube

How To Do Fraction Exponents Slide Share

Fractional Exponents Youtube

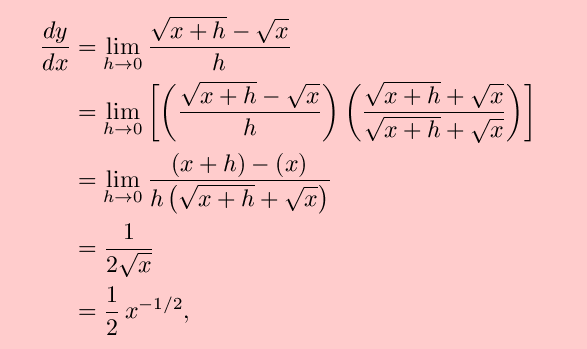
World Web Math Fractional Exponents

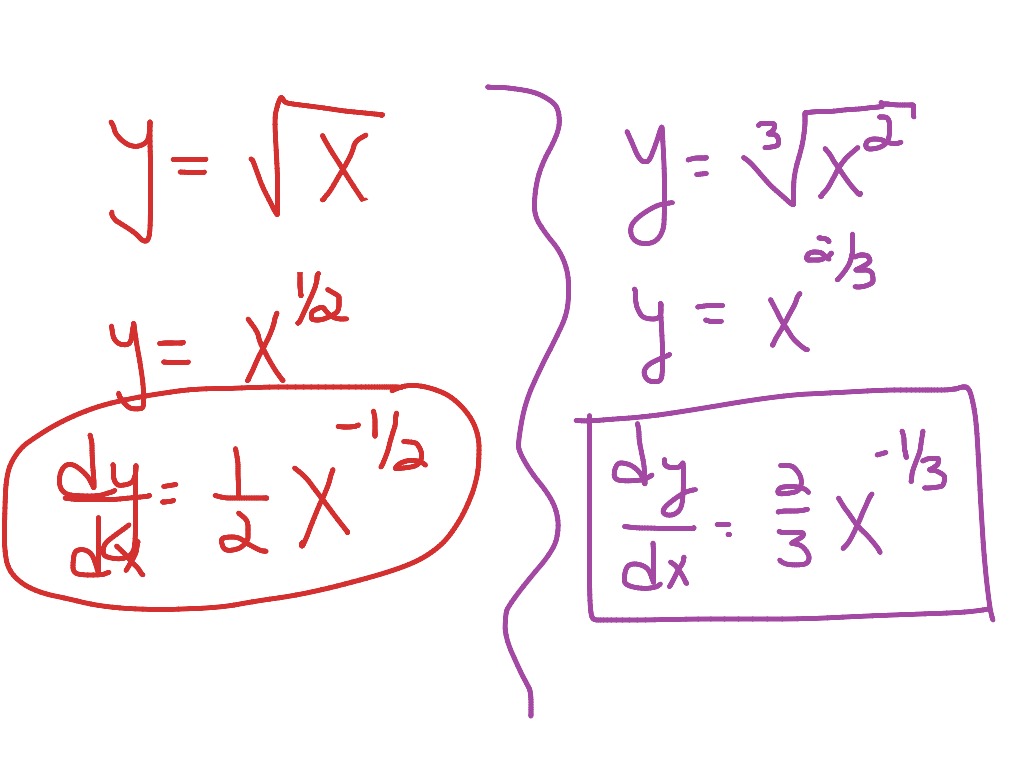
Derivatives Power Rule With Fractional Exponents Math Showme

What Are The Laws Of Rational Exponents Mathematics Stack Exchange

Rational Negative Exponents

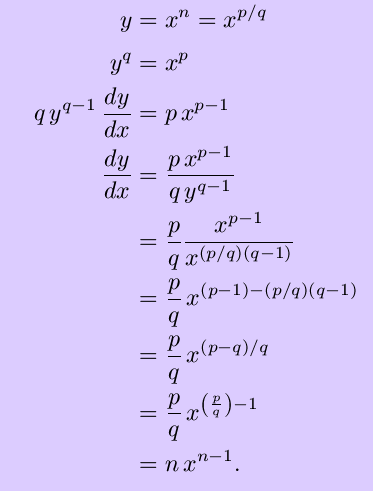
World Web Math Fractional Exponents

Rational Negative Exponents

Properties Of Rational Exponents Youtube

How To Do Fraction Exponents Slide Share

What Do Fractional Exponents Mean By Brett Berry Math Hacks Medium

What Do Fractional Exponents Mean By Brett Berry Math Hacks Medium

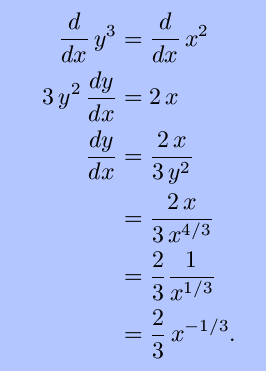
World Web Math Fractional Exponents

07 Radicals Can Be Written As Fractional Exponents Youtube